Conclusion

Conclusion

The results of all draws are:

Survey size	Methos	Sarkozy	Royal	Standard deviation
220	Simple Sampling	0.52943	0.47057	0.00993
220	Systemtic Sampling	0.53117	0.46883	0.00731
220	strata	0.53112	0.46888	0.00589
500	Simple Sampling	0.52981	0.47019	0.00527
500	Systemtic Sampling	0.52948	0.47052	0.00425
500	strata	0.52980	0.47020	0.00346

We observe two phenomena that lead a better estimate of policy variables. 

• The first is the number . Whatever the sampling method , the number of samples greatly improves the results. Knowing computing variance estimator of sampling without replacement is 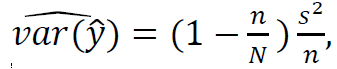 We see that over the "n" value of the number of samples increases, the variance decreases. We see a correlation between theory and practice.  
• The second is the sampling method. The simple random sampling without replacement is the easiest survey , the result is an estimate of basis for comparison . His estimate is higher than other estimates. the survey systematic sampling , we offer a better result with a practical implementation raises some question when was the result. Stratified sampling with proportional allocation of benefits lowest standard deviation between stratum alike. It is better by definition. Practice here agree well practice to theory.